“Δῶς μοι πᾶ στῶ καὶ τὰν γᾶν κινάσω“.
(Δώσε μου κάπου να σταθώ και θα κινήσω τη γη!)
Βιογραφικό
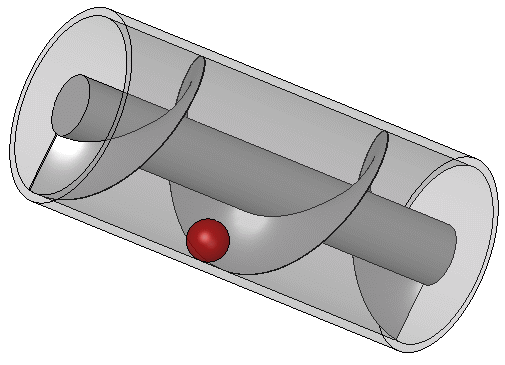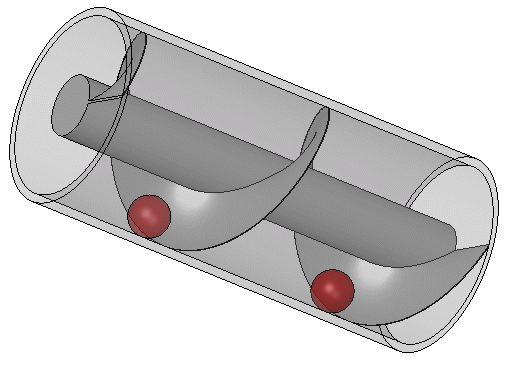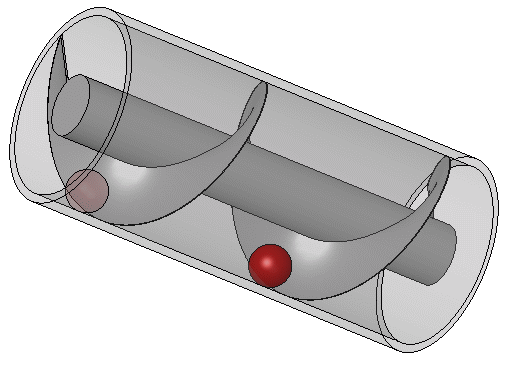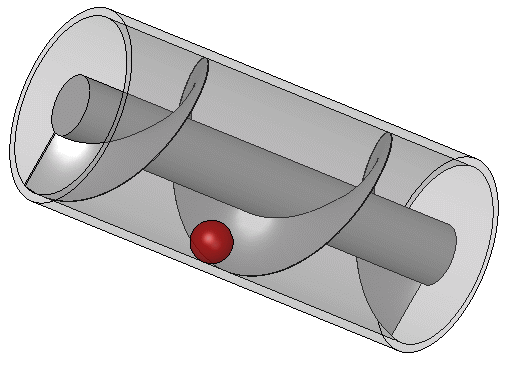
Ο Αρχιμήδηςο Συρακούσιος (Συρακούσες, Μεγάλη Ελλάδα, περ. 287 π.Χ. – Συρακούσες, Μεγάλη Ελλάδα, περ. 212 π.Χ.), αν και λίγες λεπτομέρειες είναι γνωστές για τη ζωή του, εν τούτοις θεωρούνται αρκετές ώστε σήμερα ν’ αναγνωρίζεται ως μία από τις μεγαλύτερες μαθηματικές ιδιοφυΐες όλων των εποχών κι ένας από τους λαμπρότερους επιστήμονες της κλασσικής αρχαιότητας. Η παρακαταθήκη του στη φυσική είναι, μεταξύ άλλων, οι βάσεις της υδροστατικής, της στατικής και μια εξήγηση της αρχής του μοχλού. Αυτός πιστώνεται με τον σχεδιασμό καινοτόμων μηχανών, συμπεριλαμβανομένων των πολιορκητικών μηχανών και των αντλιών με κοχλία που φέρουν το όνομά του. Αντικείμενο έρευνας έχουν αποτελέσει οι ισχυρισμοί πως σχεδίασε μηχανές ικανές να επιτίθενται σε πλοία να τα σηκώνουν έξω απ’ το νερό, και να τα πυρπολούν, χρησιμοποιώντας μια σειρά από καθρέφτες. Θεωρείται πως είναι ο σπουδαιότερος απ’ τους μαθηματικούς της αρχαιότητας κι από τους σπουδαιότερους όλων των εποχών. Στη πολιορκία των Συρακουσών σκοτώθηκε από ένα Ρωμαίο στρατιώτη, παρά τις εντολές ότι δεν έπρεπε να τον πειράξουν. Ο Κικέρων επισκέφθηκε τον τάφο του κι αναφέρει πως επιστεφόταν από μια σφαίρα εγγεγραμμένη στο εσωτερικό ενός κυλίνδρου. Ο Αρχιμήδης είχε αποδείξει ότι η επιφάνεια κι ο όγκος μιας σφαίρας είναι τα 2/3 των αντίστοιχων του περιγεγραμμένου στη σφαίρα κλειστού κυλίνδρου κι αυτό θεωρείται ως το μεγαλύτερο των μαθηματικών επιτευγμάτων του.
Το έργο του υπήρξε τεράστιο, ποιοτικά και ποσοτικά κι η ερευνητική ματιά του κάλυψε πολλούς τομείς: γεωμετρία, οπτική (κατοπτρική), υδραυλική, μηχανική, αρχιτεκτονική και την πολιορκητική. Συνέδεσε το όνομά του με τη γένεση της μηχανικής στην αρχαία Ελλάδα, τη λύση περίφημων μαθηματικών προβλημάτων, καθώς και με τις αμυντικές εφευρέσεις του που χρησιμοποιήθηκαν όταν οι Ρωμαίοι πολιορκούσανε τη πατρίδα του, τις Συρακούσες. Σχολιαστής του έργου του υπήρξεν ο Ευτόκιος ο Ασκαλωνίτης. Αντίθετα με τις εφευρέσεις του, τα μαθηματικά κείμενα του Αρχιμήδη ήταν ελάχιστα γνωστά στην αρχαιότητα. Αν και μαθηματικοί από την Αλεξάνδρεια μελέτησαν και αναφέρθηκαν σ’ αυτόν, η πρώτη κατανοητή ολοκληρωμένη συλλογή δεν ήταν έτοιμη μέχρι περίπου το 530 μ.Χ., από τον Ισίδωρο τον Μιλήσιο, ενώ σχόλια πάνω στα έργα του γράφτηκαν από τον Ευτόκιο κι αυτά γνωστοποιήθηκαν στο ευρύτερο κοινό για 1η φορά τον 6ο αι. μ.Χ.. Τα σχετικά λιγοστά αντίγραφα των γραπτών εργασιών του επιβίωσαν στον Μεσαίωνα, κι αποτελέσανε πηγή επιρροής ιδεών για τους επιστήμονες στη διάρκεια της Αναγέννησης. Η παρακαταθήκη του στη φυσική είναι, μεταξύ άλλων, βάσεις της υδροστατικής, της στατικής κι εξήγηση της αρχής του μοχλού. Πιστώνεται με το σχεδιασμό καινοτόμων μηχανών και των πολιορκητικών μηχανών και των αντλιών με κοχλία που φέρουνε τ’ όνομά του. Η ανακάλυψη το 1906 προηγούμενων άγνωστων εργασιών στο χειρόγραφο γνωστό ως Παλίμψηστο του Αρχιμήδη, παρείχε γνώσεις για το πως κατέληξε σ’ αυτά τα μαθηματικά του αποτελέσματα.
Γεννήθηκε, έζησε και πέθανε στις Συρακούσες, τη μεγάλη ελληνική αποικία της Σικελίας. Η ημερομηνία γέννησής του προκύπτει από τον Βυζαντινό ιστορικό Ιωάννη Τζέτζη, που αναφέρει πως έζησε 75 χρόνια. Στον Ψαμμίτη, ο Αρχιμήδης αναφέρει πως ο πατέρας του ονομαζόταν Φειδίας, που ήταν αστρονόμος και δεν υπάρχει τίποτα γνωστό. Αναγνωρίζεται ως μία από τις μεγαλύτερες μαθηματικές ιδιοφυΐες όλων των εποχών κι ένας από τους λαμπρότερους επιστήμονες της κλασσικής αρχαιότητας. Πατέρας του ήταν ο αστρονόμος Φειδίας ενώ συγγενής ήτανε κι ο βασιλιάς των Συρακουσών, Ιέρων Α’. Παρ’ όλο που καταγόταν από ευγενική γενιά, αρνήθηκε να πάρει οποιοδήποτε αξίωμα, επιμένοντας να διαθέτει όλο του το χρόνο στη σπουδή και τη μάθηση. Γι’ αυτό το λόγο ταξίδεψε στην Αίγυπτο κι ήρθε σε επαφή με τους Ερατοσθένη και Δοσίθεο, ενώ ήτανε φίλος και συμμαθητής του Κόνωνα του Σάμιου.

Ο Πλούταρχος έγραψε στο έργο του Βίοι Παράλληλοι ότι ο Αρχιμήδης ήταν συγγενής και φίλος με τον βασιλιά Ιέρωνα τον Β’, τον κυβερνήτη των Συρακουσών. Μια βιογραφία του είχε γραφτεί από τον φίλο του Ηρακλείδη, αλλά η εργασία του αυτή έχει χαθεί, αφήνοντας τις λεπτομέρειες της ζωής του στο σκοτάδι. Είναι άγνωστο, για παράδειγμα, αν είχε ποτέ παντρευτεί ή είχε παιδιά. Στη νεότητα του, μπορεί να ‘χε σπουδάσει στην Αλεξάνδρεια της Αιγύπτου, όπου ο Κόνωνας ο Σάμιος κι ο Ερατοσθένης ο Κυρηναίος ήτανε σύγχρονοί του. Αναφέρει τον Κόνωνα ως φίλο και 2 απ’ τα έργα του (μέθοδος μηχανολογικών θεωρημάτων και Πρόβλημα των βοοειδών) έχουν εισαγωγή που απευθύνεται στον Ερατοσθένη.
Έγραψε τα 1α βιβλία για την επίπεδη γεωμετρία και στερεομετρία, την αριθμητική και τα μαθηματικά. Επίσης ανακάλυψε την αρχή του ειδικού βάρους και του μοχλού. Μία μέρα ο βασιλιάς παρήγγειλε στο μεγαλύτερο καλλιτέχνη των Συρακουσών να του φτιάξει μία κορώνα από καθαρό χρυσάφι. Όταν ο βασιλιάς πήρε τη κορώνα, άρχισαν να διαδίδονται φήμες πως ο καλλιτέχνης τον είχε κοροϊδέψει, παίρνοντας ένα μέρος από το χρυσάφι και αντικαθιστώντας το με άλλο μέταλλο. Ωστόσο, η τελειωμένη κορώνα είχε το ίδιο βάρος με το χρυσάφι του βασιλιά. Ο βασιλιάς κάλεσε τότε τον Αρχιμήδη να εξετάσει το ζήτημα. Στα πειράματά του, βρήκε τον νόμο του ειδικού βάρους. Ανακάλυψε πως όταν ένα στερεό σώμα μπει μέσα σε υγρό χάνει τόσο βάρος όσο είναι το βάρος του όγκου του νερού που εκτοπίζει. Επινόησε το σύστημα να παίρνει το ειδικό βάρος των στερεών σωμάτων. Ζύγιζε πρώτα το στερεό στον αέρα κι έπειτα το ζύγιζε στο νερό. Κι αφού το στερεό ζύγιζε λιγότερο στο νερό, αφαιρούσε το βάρος που είχε στο νερό από το βάρος που είχε στον αέρα. Τέλος, διαιρούσε το βάρος του στερεού σώματος στον αέρα με την απώλεια βάρους που είχε το σώμα μέσα στο νερό. Έμαθε έτσι, πως ένας δοσμένος όγκος από χρυσάφι ζυγίζει 19,3 φορές τον ίσο όγκο νερού. Όμως, καθώς δεν μπόρεσε να προχωρήσει περισσότερο στο πρόβλημα της βασιλικής κορώνας, πήγε στα λουτρά για να ξεκουραστεί. Εκεί βρήκε τη λύση. Μες στον ενθουσιασμό του βγήκε από το λουτρό γυμνός στο δρόμο φωνάζοντας: “Εύρηκα! Εύρηκα!“. Γύρισε στο σπίτι, ζύγισε τη κορώνα στον αέρα κι ύστερα τη ζύγισε στο νερό. Με τη μέθοδο αυτή βρήκε το ειδικό βάρος της κορώνας. Το ειδικό βάρος της δεν ήτανε 19,3. Δε μπορούσε, λοιπόν, η κορώνα να ‘ναι από καθαρό χρυσό. Ο Αρχιμήδης απέδειξε πως ο καλλιτέχνης ήταν απατεώνας.
Η αποκάλυψη ενός απατεώνα ήτανε πολύ μικρή εξυπηρέτηση σε σύγκριση με κείνες που θα προσέφερε αργότερα στο βασιλιά του. Όταν άρχισαν να κυκλοφορούν στις Συρακούσες φήμες πως οι Ρωμαίοι βάδιζαν εναντίον τους, ο Αρχιμήδης εξακολουθούσε τις μελέτες και τις εφευρέσεις. Σ’ αυτή τη περίοδο και στο χώρο της εφαρμοσμένης μηχανικής, ο Αρχιμήδης επινόησε ιδιοφυείς μηχανές κάθε είδους. Εφηύρε τον ρωμαϊκό ζυγό (καντάρι), το τρίσπαστο (ανυψωτική 3πλή τροχαλία) και τον ατέρμονα κοχλία (έλιξ του Αρχιμήδους), που ήτανε σωληνοειδής κοχλίας που χρησίμευε για την άντληση νερού. Επίσης κατασκεύασε υδραυλικό ρολόι που υπολόγιζε με μεγάλη ακρίβεια τις ώρες κι ειδοποιούσε για την αλλαγή της ώρας.
Όταν άρχισε η πολιορκία των Συρακουσών από τους Ρωμαίους, οι πολεμικές μηχανές του Αρχιμήδη αποδείχτηκαν εξαιρετικά χρήσιμες: αρχιτρόνιτο (πυροβόλο ατμού), καταπέλτες, άρπαγες (μηχανισμός που ανύψωνε κι αναποδογύριζε πλοία) και κάτοπτρα για τη καύση των Ρωμαϊκών εχθρικών πλοίων (με παραβολικά ηλιακά κάτοπτρα όπως αποδείχτηκε από τα πειράματα του μηχανικού Ιωάννη Σακκά, που το 1973 απέδειξε τον τρόπο που έκαψε τον ρωμαϊκό στόλο). Ωστόσο οι Ρωμαίοι όλο και πλησίαζαν. Ο Αρχιμήδης μισούσε τους εισβολείς αλλά δεν τους φοβότανε. Σύμφωνα με τη παράδοση, όταν η πόλη μετά από 3ετή αντίσταση των Ελλήνων, κατελήφθη με προδοσία, ένας Ρωμαίος στρατιώτης μπήκε στο σπίτι του Αρχιμήδη την ώρα που μελετούσε κάποιο γεωμετρικό πρόβλημα. Ο Αρχιμήδης είπε στον στρατιώτη να βγει έξω και να μη διαταράξει τη σκέψη του, λέγοντάς το περίφημο “Μη μου τους κύκλους τάραττε“. Όμως ο στρατιώτης έβγαλε το σπαθί και τονε σκότωσε.
Ο Αρχιμήδης αγαπούσε τόσο πολύ την εργασία του Περί Σφαίρας και Κυλίνδρου, ώστε είπε ότι θα ‘θελε όταν πεθάνει να χαραχτεί στον τάφο του το σχήμα μιας σφαίρας εγγεγραμμένης σε κύλινδρο. Ο κατακτητής Μάρκελλος είχε αναπτύξει τέτοιο θαυμασμό κι εκτίμηση για τον Αρχιμήδη ως αντίπαλο, ώστε όταν έμαθε πως σκοτώθηκε, τον έθαψε με μεγάλη μεγαλοπρέπεια και τελετές κι έστησε στον τάφο του μια πέτρινη στήλη που πάνω της ήτανε σκαλισμένο το σχήμα που είχε ζητήσει ο Αρχιμήδης. Πολλά έτη μετά, όταν ο Κικέρων επισκέφτηκε τις Συρακούσες σα Ρωμαίος έφορος, κανείς δεν ήξερε να τον οδηγήσει στον τάφο του Αρχιμήδη. Μετά από πολλές έρευνες βρήκε τη ταφόπετρα ανάμεσα σε ψηλούς βάτους κι έφτιαξε ξανά το έδαφος γύρω από τον τάφο. Με το πέρασμα του χρόνου όμως, ο τάφος παραμελήθηκε κι όλα δείχνανε πως με την αύξηση της πόλης ο τάφος θα χανόταν οριστικά. Όμως το 1965, σκάβοντας για τη θεμελίωση ενός νέου ξενοδοχείου στις Συρακούσες, ένας εκσκαφέας σήκωσε μία ταφόπετρα με σκαλισμένο πάνω της το σχήμα μιας σφαίρας εγγεγραμμένης σε κύλινδρο σκαλισμένο. Έτσι ανακαλύφτηκε ο τάφος του.

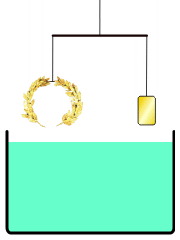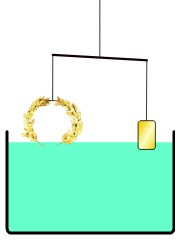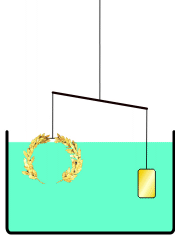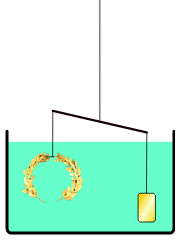
Ο Αρχιμήδης επηρέασε σε μεγάλο βαθμό την ευρωπαϊκή επιστημονική σκέψη, καθώς και τους Άραβες επιστήμονες, που αντέγραψαν όλα τα έργα του στα αραβικά, γλώσσα που διασώθηκαν αρκετά, αφού τα πρωτότυπα είχανε χαθεί. Η πιο γνωστή του ιστορία αφορά στη μέθοδο που εφηύρε για το προσδιορισμό του όγκου ενός αντικειμένου με ακανόνιστο σχήμα. O βασιλιάς Ιέρων Β’ είχε παραγγείλει να του φτιάξουν ένα αναθηματικό στέμμα από ατόφιο χρυσάφι. Επειδή δεν είχε εμπιστοσύνη στο χρυσοχόο, ζήτησε από τον Αρχιμήδη να εξετάσει αν ο χρυσός είχε νοθευτεί με ασήμι. Επειδή ο Αρχιμήδης έπρεπε να λύσει το πρόβλημα χωρίς να καταστρέψει το στέμμα, δεν μπορούσε να το λυώσει προκειμένου να υπολογίσει τη πυκνότητα και τη προέλευσή του. Καθώς έκανε μπάνιο, παρατήρησε πως η στάθμη του νερού στη μπανιέρα ανέβηκε όταν μπήκε ο ίδιος μέσα και συνειδητοποίησε πως αυτό θα μπορούσε να χρησιμοποιηθεί για το προσδιορισμό του όγκου του στέμματος. Με τη παραδοχή ότι το νερό πρακτικά είναι ασυμπίεστο, το αποτέλεσμα της βύθισης θα ήταν το στέμμα να εκτοπίσει μια ποσότητα νερού ίση με τον δικό του όγκο. Διαιρώντας τη μάζα του στέμματος με τον όγκο του νερού που εκτοπίζεται προκύπτει η πυκνότητα του στέμματος. Αυτή η πυκνότητα θα ‘ναι μικρότερη από κείνη του χρυσού, αν κάποια φθηνότερα και λιγότερο πυκνά μέταλλα είχαν προστεθεί. Ο Αρχιμήδης ενθουσιάστηκε τόσο από την ανακάλυψή του ώστε βγήκε στον δρόμο γυμνός φωνάζοντας “Εύρηκα! Εύρηκα!”. Η εξέταση του στέμματος απέδειξε ότι είχε νοθευτεί με σίδερο.
Η Αρχή του Αρχιμήδη καθορίζει ότι: “Κάθε σώμα βυθισμένο σε ρευστό δέχεται άνωση ίση με το βάρος του ρευστού που εκτοπίζει“. Όταν το βάρος ενός σώματος είναι μεγαλύτερο από την άνωση που αυτό δέχεται τότε θα βυθιστεί, ενώ σε αντίθετη περίπτωση θα επιπλέει. Η Αρχή του Αρχιμήδη βρίσκει μεγάλη εφαρμογή στη καθημερινή ζωή. Οτιδήποτε πλέει, όπως τα πλοία, όλα τα ελαφρύτερα του ύδατος σώματα, το ανθρώπινο σώμα, οι πλωτήρες, αμφίβια οχήματα κλπ. υπακούουνε στην Αρχή αυτή. Πιότερο όμως ενδιαφέρει η Αρχή αυτή τη Ναυπηγική, δηλαδή την επιστήμη που ασχολείται με τη κατασκευή πλοίων. Εκεί η Αρχή του Αρχιμήδη μελετάται, αναλύεται κι εφαρμόζεται σ’ όλες τις λεπτομέρειές της.
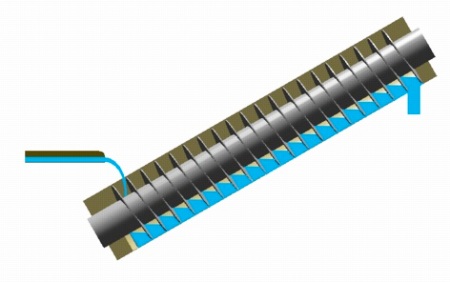
Ο Κοχλίας Του Αρχιμήδη
Ο Kοχλίας του Αρχιμήδη, ή αντλία με κοχλία, είναι μια κατασκευή που από την αρχαιότητα χρησιμοποιείτο για ν’ αντλεί και να μετακινεί νερό από κάποιο χαμηλό μέρος κυρίως σε κανάλια άρδευσης. Η εφεύρεση της αντλίας με κοχλία (βίδα) αποδίδεται στον Αρχιμήδη. Μεγάλο μέρος του έργου του στη μηχανική προέκυψε από την ικανοποίηση των αναγκών της γενέτειρας πόλης, των Συρακουσών. Ο Αθηναίος αναφέρει πώς ο βασιλιάς Ιέρων Β’ ανέθεσε στον Αρχιμήδη να σχεδιάσει ένα τεράστιο πλοίο, τη Συρακουσία, που θα μπορούσε να χρησιμοποιηθεί για ταξίδια αναψυχής, για μεταφορά προμηθειών κι ως πολεμικό πλοίο. Σύμφωνα με τον Αθήναιο πάντα, ήταν ικανό να μεταφέρει 600 άτομα και περιλάμβανε διακοσμητικούς κήπους, γυμναστήριο και ναό αφιερωμένο στη θεά Αφροδίτη. Δεδομένου ότι σε πλοίο αυτού του μεγέθους θα διέρρεε σημαντική ποσότητα νερού διαμέσου του κύτους, ο κοχλίας εικάζεται ότι αναπτύχθηκε με σκοπό την απομάκρυνση του νερού. Ο μηχανισμός συνίστατο σε περιστρεφόμενο κοχλία σε σχήμα λεπίδας μέσα σε κύλινδρο (ελικοειδής επιφάνεια μέσα σε κύλινδρο). Γυρνούσε χειροκίνητα και μπορούσε επίσης να χρησιμοποιηθεί για τη μεταφορά νερού από ένα χαμηλού επίπεδου σώμα του νερού σε κανάλια άρδευσης. Είναι ακόμα σε χρήση σήμερα για την άντληση υγρών και στερεών σε κόκκους, όπως ο άνθρακας και το σιτάρι. Ο κοχλίας περιστρέφεται μέσω ενός ανεμόμυλου ή ακόμα και χειροκίνητα, βρίσκεται σε κλίση με το έδαφος και καθώς γυρίζει, ποσά νερού εγκλωβίζονται και μεταφέρονται μέχρι το πάνω μέρος της κατασκευής, απ’ όπου το νερό χύνεται και τροφοδοτεί κανάλια άρδευσης. Ο κοχλίας όπως περιγραφότανε στα ρωμαϊκά έτη από το Βιτρούβιο, μπορεί να ‘τανε βελτίωση σε σχέση με αντλία-κοχλία που ‘χε χρησιμοποιηθεί για την άρδευση των Κρεμαστών Κήπων της Βαβυλώνας. Το 1ο στον κόσμο ατμόπλοιο με βιδωτή έλικα ήταν το SS Archimedes, που ξεκίνησε να λειτουργεί το 1839 κι ονομάστηκε έτσι προς τιμή του έργου του πάνω στον κοχλία.
Η Αρπάγη του Αρχιμήδη ήταν πολεμικό όπλο που επινόησε για την αντιμετώπιση του ρωμαϊκού στόλου που πολιορκούσε τις Συρακούσες. Δεν υπάρχουν αρχαιολογικά ευρήματα ή απεικονίσεις της κατασκευής. Την αναφέρουν οι αρχαίοι ιστορικοί περιγράφοντάς την ως είδος γερανού μ’ αγκίστρι. Φαίνεται πως ήταν εφαρμογή των μελετών του γύρω από τους μοχλούς και τις τροχαλίες. Στις σημερινές μας ημέρες μια επιστημονική ομάδα το 1999 επιχείρησε ένα πείραμα κατασκευής και χρήσης μιας αρπάγης. Μέσα σε 7 μέρες σχεδίασαν, κατασκεύασαν και χρησιμοποίησαν μ’ επιτυχία μιαν αρπάγη που στο πείραμα αυτό τελικά αναποδογύρισε και βύθισε μια τριήρη στο λιμάνι μπρος στα αρχαία τείχη των Συρακουσών. Λέγεται πως είχε σχεδιαστεί για την άμυνα των Συρακουσών. Επίσης γνωστή ως αναδευτής πλοίων, η αρπάγη απετελείτο από βραχίονα-γερανό, απ’ όπου αναπτυσσόταν μεγάλος μεταλλικός γάντζος. Όταν η αρπάγη θα ‘πεφτε πάνω στο επιτιθέμενο πλοίο ο βραχίονας θα ταλαντευόταν προς τα πάνω, τραβώντας το πλοίο έξω από το νερό και προκαλώντας τη βύθισή του. Υπήρξαν σύγχρονα πειράματα για να ελεγχθεί η σκοπιμότητα της Αρπάγης και το 2005 ένα τηλεοπτικό ντοκιμαντέρ με τίτλο Υπερόπλα του αρχαίου κόσμου, κατασκεύασε έκδοση της Αρπάγης και κατέληξε στο συμπέρασμα ότι ήτανε λειτουργική συσκευή.
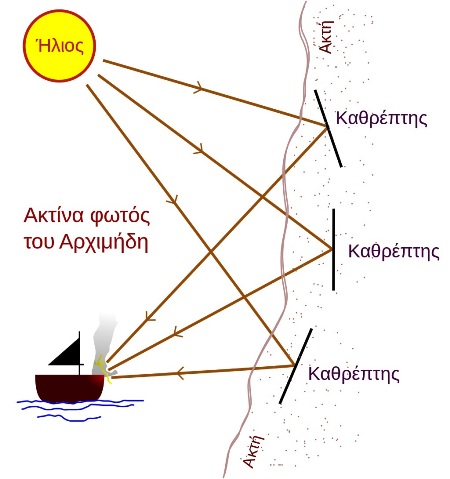
Η Θερμική ακτίνα φωτός του Αρχιμήδη ήτανε συσκευή που χρησιμοποίησε για να κάψει επιτιθέμενα ρωμαϊκά πλοία στη διάρκεια της πολιορκίας των Συρακουσών. Περιγράφεται από ιστορικούς που την αναφέρουνε πολλά χρόνια μετά τη πολιορκία. Το 2ο αι. μ.Χ. ο συγγραφέας Λουκιανός έγραψε ότι στη διάρκεια της Πολιορκίας των Συρακουσών (214-212 π.Χ.), ο Αρχιμήδης κατέστρεψε εχθρικά πλοία με τη χρήση της φωτιάς. Αιώνες αργότερα, ο Ανθέμιος ο Τραλλιανός αναφέρει το φλεγόμενο γυαλί ως το όπλο του Αρχιμήδη. Η συσκευή, γνωστή κι ως Ακτίνα Φωτός του Αρχιμήδη, χρησιμοποιείτο για να συγκεντρώνει το ηλιακό φως στα επερχόμενα πλοία, με αποτέλεσμα αυτά να παίρνουνε φωτιά. Αυτό το υποτιθέμενο όπλο υπήρξε θέμα συνεχόμενης διαμάχης από την Αναγέννηση. Ο Ρενέ Ντεκάρτ το απέρριψε ως λανθασμένο, ενώ νέες έρευνες έχουν αποπειραθεί ν’ αναπαραστήσουνε το αποτέλεσμα χρησιμοποιώντας μόνο τα μέσα που ήτανε διαθέσιμα στον Αρχιμήδη. Έχει προταθεί ότι μεγάλη παράταξη από αρκετά γυαλισμένες μπρούτζινες ή χάλκινες ασπίδες που λειτουργούσανε σαν καθρέπτες θα μπορούσαν να ‘χανε χρησιμοποιηθεί για να συγκεντρώσουνε το ηλιακό φως στο πλοίο. Αυτό βασιζότανε στην αρχή του παραβολικού κατόπτρου με παρόμοιο τρόπο όπως σ’ έναν ηλιακό φούρνο. Δοκιμή της ακτίνας φωτός του Αρχιμήδη έγινε το 1973 από τον Έλληνα επιστήμονα Ιωάννη Σάκκα. Το πείραμα έλαβε χώρα στη ναυτική βάση του Σκαραμαγκά έξω από την Αθήνα. Γι’ αυτό χρησιμοποιήθηκαν 70 καθρέπτες, ο καθένας με χάλκινη επίστρωση και μέγεθος περίπου στα 1,5χ1 m. Οι καθρέπτες στραφήκανε σε ομοίωμα από κόντρα πλακέ ενός ρωμαϊκού πολεμικού πλοίου που βρισκότανε σε απόσταση κοντά στα 50 m. Όταν οι καθρέπτες σημάδεψαν με ακρίβεια το πλοίο, αυτό έπιασε φωτιά μέσα σε λίγα δευτερόλεπτα. Το πλοίο από κόντρα πλακέ ήταν επιστρωμένο με βαφή πίσσας, που μπορεί να βοήθησε στην ανάφλεξη. Η επίστρωση με βαφή πίσσας ήτανε κοινότοπη στα πλοία τη κλασσική εποχή.
Οκτώβρη του 2005, ομάδα φοιτητών του Τεχνολογικού Ινστιτούτου Μασαχουσέτης διεξήγαγε ένα πείραμα με 127 τετραγωνικά κεραμίδια καθρέπτη 30 cm, στοχεύοντας ένα ομοίωμα ξύλινου πλοίου σε απόσταση περίπου 30 m. Φλόγες ξεσπάσανε σε μπάλωμα του πλοίου αλλά μόνον όταν ο ουρανός δεν είχε σύννεφα και το πλοίο παρέμεινε στη θέση του για περίπου 10 λεπτά. Προέκυψε το συμπέρασμα ότι η παράταξη ήταν ένα εφικτό όπλο κάτω από αυτές τις συνθήκες. Η ομάδα επανέλαβε το πείραμα για τη τηλεοπτική εκπομπή MythBusters, χρησιμοποιώντας ξύλινη βάρκα ψαρέματος στο Σαν Φρανσίσκο, ως στόχο. Ξανά συνέβη μερική απανθράκωση, μαζί με μικρή φωτιά. Για να πιάσει φωτιά, το ξύλο χρειάζεται να φτάσει στη θερμοκρασία αυτανάφλεξης, που είναι γύρω στους 300 °C.
Όταν οι Mythbusters προβάλανε το αποτέλεσμα του πειράματος στο Σαν Φρανσίσκο, Γενάρη του 2006, ο μύθος τοποθετήθηκε στη κατηγορία των κατερριμμένων λόγω του χρόνου και των ιδανικών καιρικών συνθηκών που χρειαζότανε για να συμβεί η ανάφλεξη. Επίσης τονίστηκε πως αφού οι Συρακούσες έβλεπαν τη θάλασσα προς τα ανατολικά, ο ρωμαϊκός στόλος θα ‘πρεπε να επιτεθεί στη διάρκεια του πρωινού για βέλτιστη συγκέντρωση φωτός από τους καθρέπτες. Οι Mythbusters τόνισαν επίσης ότι συμβατικά όπλα όπως φλεγόμενα βέλη ή βίδες από τους καταπέλτες θα ήταν ένας πολύ εύκολος τρόπος για να βάλουν φωτιά σε ένα πλοίο σε κοντινές αποστάσεις. Δεκέμβρη του 2010, οι Mythbusters άνοιξαν ξανά την υπόθεση της ακτίνας φωτός σε σπέσιαλ επεισόδιο όπου συμμετείχε κι ο Μπαράκ Ομπάμα με τον τίτλο Η πρόκληση του προέδρου. Αρκετά πειράματα διεξήχθησαν, συμπεριλαμβανομένης και μιας δοκιμής μεγάλης κλίμακας με 500 μαθητές να σημαδεύουν με τους καθρέπτες ομοίωμα ενός ρωμαϊκού πλοίου σε απόσταση 120 m. Σε όλα τα πειράματα το ιστίο απέτυχε να φτάσει στους 210 °C που απαιτούνται για να πιάσει φωτιά κι ο μύθος τοποθετήθηκε εκ νέου στη κατηγορία των κατερριμένων. Η εκπομπή συμπέρανε πως ένα πιο πιθανό αποτέλεσμα των καθρεφτών θα ήταν να τυφλώνει, να εκθαμβώνει και ν’ αποσπά τη προσοχή του πληρώματος του πλοίου.
Μολονότι δεν ήταν ο Αρχιμήδης που εφηύρε τον μοχλό, εκείνος έδωσε μια εξήγηση για την αρχή που βασίζεται η χρήση του. Το έργο του πάνω στους μοχλούς τον έκανε να πει: “Δώστε μου ένα σημείο να στηριχθώ και θα κινήσω τη Γη“. (δῶς μοι πᾶ στῶ καὶ τὰν γᾶν κινάσω).
Ο Πλούταρχος περιγράφει πώς ο Αρχιμήδης σχεδίαζε ανυψωτικά συστήματα τροχαλιών επιτρέποντας στους ναυτικούς να χρησιμοποιούνε την αρχή της μόχλευσης για να σηκώνουν αντικείμενα που ειδάλλως δεν θα μπορούσαν να σηκώσουν. Στον Αρχιμήδη επίσης αποδίδεται η βελτίωση της δύναμης και της ακρίβειας του καταπέλτη καθώς κι η εφεύρεση του οδομετρητή στη διάρκεια του Α’ Καρχηδονιακού Πολέμου. Ο οδομετρητής περιγράφεται ως ένα κάρρο με μηχανισμό γραναζιού που έριχνε μια μπάλα σ’ ένα κιβώτιο κάθε φορά που συμπλήρωνε ένα μίλι. Κατασκεύασε επίσης υδραυλικό ρολόι που υπολόγιζε με μεγάλη ακρίβεια τις ώρες κι ειδοποιούσε για την αλλαγή της ώρας. Ενώ συχνά θεωρείται ως σχεδιαστής μηχανικών συσκευών, ο Αρχιμήδης είχε επίσης συνεισφορές στον τομέα των μαθηματικών. Χρησιμοποίησε το πυθαγόρειο θεώρημα για να υπολογίσει την πλευρά του 12γώνου απ’ αυτή του 6γώνου και για κάθε επακόλουθο διπλασιασμό των πλευρών του κανονικού πολυγώνου.
Με τη μέθοδο της εξάντλησης που εφάρμοσε κατάφερε να προσεγγίσει τη τιμή του αριθμού π (=3,14). Στο Κύκλου Μέτρησις το ‘κανε αυτό ζωγραφίζοντας ένα μεγαλύτερο κανονικό 6άγωνο έξω από τον κύκλο κι ένα μικρότερο κανονικό 6άγωνο μες στο κύκλο και προοδευτικά διπλασιάζοντας τον αριθμό των πλευρών και στα 2 κανονικά πολύγωνα, υπολογίζοντας το μήκος της πλευράς κάθε πολυγώνου σε κάθε βήμα. Όσον ο αριθμός των πλευρών αυξάνεται γίνεται πιο ακριβής προσέγγιση του κύκλου. Ο Αρχιμήδης προσέγγισε (χωρίς να διευκρινίσει πώς) τη τετραγωνική ρίζα του 3 που η πραγματική τιμή της είναι 1,7320508.
—————–
Για την απομνημόνευση των πρώτων λίγων δεκαδικών ψηφίων του αριθμού π, που ανακάλυψε πρώτα ο Αρχιμήδης, έχουν επινοηθεί διάφοροι μνημονικοί κανόνες. Με αυτήν μπορεί κανείς να θυμάται τα πρώτα 22 δεκαδικά ψηφία του:
Αεί ο Θεός ο Μέγας γεωμετρεί, 3, 1 4 1 5 9
το κύκλου μήκος ίνα ορίση διαμέτρω, 2 6 5 3 5 8
παρήγαγεν αριθμόν απέραντον, 9 7 9
και ον, φεύ, ουδέποτε όλον θνητοί θα εύρωσι. 3 2 3 8 4 6 2 6
Το πλήθος των γραμμάτων κάθε λέξης της φράσης αυτής αντιστοιχεί σε καθένα από τα διαδοχικά ψηφία του αριθμού π.
_____________________
Ο Αρχιμήδης πέθανε το 212 π.Χ. στη διάρκεια του Β’ Καρχηδονιακού Πολέμου, όταν οι ρωμαϊκές δυνάμεις υπό τον στρατηγό Μάρκο Κλαύδιο Μάρκελλο κυριέυσανε τη πόλη μετά από πολιορκία 2 ετών. Σύμφωνα με τον Πλούταρχο, ο Αρχιμήδης είχε κατά νου ένα μαθηματικό διάγραμμα όταν η πόλη είχε καταληφθεί και δεν είχε αντιληφθεί την άλωση της. Οι τελευταίες λέξεις που του αποδίδονται είναι “μην ενοχλείτε τους κύκλους μου” (μή μου τοὺς κύκλους τάραττε), αναφερόμενος στους κύκλους στο μαθηματικό του σχέδιο που υποτίθεται ότι μελετούσε όταν τον διέκοψε ο Ρωμαίος στρατιώτης (συχνά τιμητικά αποδίδεται στα λατινικά ως Noli turbare circulos meos, αλλά δεν υπάρχουν αξιόπιστα στοιχεία πως πρόφερε αυτές τις λέξεις και δεν εμφανίζονται στα γραπτά που μας έχουνε διασωθεί απ’ τον Πλούταρχο). Ο Ρωμαίος τονε διέταξε να πάει και να συναντήσει τον στρατηγό Μάρκο Κλαύδιο Μάρκελλο αλλά αυτός αρνήθηκε λέγοντας ότι έπρεπε να τελειώσει με το πρόβλημα του. Ο στρατιώτης εξοργίστηκε και τονε σκότωσε με το σπαθί του.
Μια 2η εκδοχή που δίνει ο Πλούταρχος είναι ότι καθώς ο Ρωμαίος στρατιώτης ορμούσε κατά πάνω του με γυμνό το ξίφος, ο Αρχιμήδης τον παρακάλεσε, μάταια όμως, να περιμένει λίγο ώστε να μη μείνει άλυτο το πρόβλημα που τον απασχολούσε. Και μια 3η εκδοχή του Πλουτάρχου είναι ότι ο Αρχιμήδης μεταβαίνοντας προς τον Μάρκελλο είχε μαζί του μαθηματικά όργανα και τονε σκοτώσανε στρατιώτες επειδή νόμιζαν ότι ήταν πολύτιμα αντικείμενα. Ο Μάρκελλος όταν πληροφορήθηκε τον θάνατο του Αρχιμήδη λυπήθηκε πολύ καθώς τονε θεωρούσε ως ένα πολύτιμο κεφάλαιο για την επιστήμη κι είχε διατάξει να μη πειραχτεί, εξοργίστηκε με τον στρατιώτη κι ευεργέτησε τους οικείους του Αρχιμήδη.
Τα έργα του Αρχιμήδη είχαν γραφτεί στη δωρική διάλεκτο, τη διάλεκτο των αρχαίων Συρακουσών. Τα γραπτά έργα του δεν έχουνε διασωθεί όπως αυτά του Ευκλείδη κι 7 από τις πραγματείες του είναι γνωστό ότι υπήρχαν μόνο μέσα από αναφορές που γίνονται σ’ αυτές από άλλους συγγραφείς. Ο Πάππος ο Αλεξανδρεύς αναφέρει το έργο του Περί σφαιροποιΐας καθώς κι ένα άλλο πάνω στα πολύεδρα, ενώ ο Θέων ο Αλεξανδρεύς κάνει μία παρατήρηση σχετικά με τη διάθλαση από το μη διασωθέν σήμερα έργο του Κάτοπτρα. Στη διάρκεια της ζωής του, ο Αρχιμήδης έκανε το έργο του γνωστό μέσω αλληλογραφίας με τους μαθηματικούς στην Αλεξάνδρεια. Τα γραπτά του Αρχιμήδη συλλέχθηκαν από αρχιτέκτονα της Βυζαντινής Αυτοκρατορίας τον Ισίδωρο τον Μιλήσιο (~530 μ.Χ.), ενώ τα σχόλια για τα έργα του γραμμένα από τον Ευτόκιο στον 6ο μ.Χ. αι., βοήθησαν να διαδοθεί το έργο του σ’ ευρύτερο κοινό. Έργο του Αρχιμήδη μεταφράστηκε στα αραβικά από τον Ταμπίτ ιμπν Κουρά (836-901 μ.Χ.), και στη λατινική από το Γεράρδο της Κρεμόνα (περ. 1114-1187 μ.Χ.). Στη διάρκεια της Αναγέννησης, η Editio Princeps (1η έκδοση), δημοσιεύθηκε στη Βασιλεία το 1544 από τον Johann Herwagen, με τα έργα του Αρχιμήδη στην ελληνική και λατινική. Το έτος 1586, ο Γαλιλαίος Γαλιλέι εφηύρε υδροστατικό ζυγό για τη ζύγιση των μετάλλων στον αέρα και στο νερό, εμπνευσμένος προφανώς από το έργο του Αρχιμήδη.

Ο τάφος του Αρχιμήδη είχε ένα γλυπτό που απεικόνιζε την αγαπημένη μαθηματική απόδειξη του, αποτελούμενη από μία σφαίρα κι ένα κύλινδρο με το ίδιο ύψος και διάμετρο. Είχε αποδείξει ότι το εμβαδόν κι ο όγκος μιας σφαίρας είναι τα 2/3 του κλειστού κυλίνδρου που τη περιβάλλει συμπεριλαμβανομένων και των βάσεων του κυλίνδρου. Το 75 π.Χ., 137 χρόνια μετά το θάνατό του, ο Ρωμαίος ρήτορας Κικέρων υπηρετούσε ως κυαίστορας στη Σικελία. Είχε ακούσει ιστορίες για τον τάφο του Αρχιμήδη, αλλά κανείς από τους ντόπιους δεν ήτανε σε θέση να προσδιορίσει τη θέση του τάφου. Ενδεχομένως βρήκε τον τάφο κοντά στην Ακραγαντινή πύλη των Συρακουσών, σε παραμελημένη κατάσταση και κατάφυτη από θάμνους. Ο Κικέρων διέταξε να καθαρίσουν τον τάφο κι ήτανε σε θέση να δει το σκάλισμα και να διαβάσει μερικά από τα εδάφια, που είχανε προστεθεί ως επιγραφή. Ένα ελληνιστικό μαυσωλείο, που ανακαλύφθηκε στην αυλή ενός ξενοδοχείου που ανεγέρθη στις Συρακούσες στις αρχές του 1960, θεωρήθηκε από τον Ciancio ότι είναι ο τάφος του Αρχιμήδη. Αλλά ο ανασκαφέας, ο έφορος αρχαιοτήτων Συρακουσών, Gentili, προτείνει τη ταύτιση με ένα σημαντικό πρόσωπο της εποχής του Αγαθοκλέους (ίσως του ίδιου του βασιλέα).
Οι βασικές εκδοχές της ζωής του Αρχιμήδη γράφτηκαν πολύ καιρό μετά το θάνατό του από τους ιστορικούς της αρχαίας Ρώμης. Ο απολογισμός της πολιορκίας των Συρακουσών δίνεται από τον Πολύβιο στις Ιστορίες του που γράφτηκαν 70 έτη μετά το θάνατό του και χρησιμοποιηθήκανε στη συνέχεια ως πηγή από τον Πλούταρχο και τον Λίβιο. Αυτός έδωσε πληροφορίες για τον Αρχιμήδη ως πρόσωπο κι επικεντρώθηκε στις πολεμικές μηχανές που λέγεται πως είχανε κατασκευαστεί για να υπερασπίσουνε τη πόλη.
Ο Κικέρων πάλι, αναφέρει εν συντομία τον Αρχιμήδη στο διάλογό του Περί δημοκρατίας, που απεικονίζει μια φανταστική συζήτηση που λαμβάνει χώρα το 129 π.Χ.. Μετά τη κατάκτηση των Συρακουσών το 212 π.Χ. λέγεται ότι ο Στρατηγός Μάρκος Κλαύδιος Μάρκελλος πήρε πίσω στη Ρώμη δύο μηχανισμούς, που κατασκευάσθηκαν από τον Αρχιμήδη και μ’ εφαρμογή στην αστρονομία, που έδειχνε την κίνηση του Ηλίου, της Σελήνης και 5 πλανητών. Ο Κικέρων αναφέρει παρόμοιους μηχανισμούς σχεδιασμένους από το Θαλή τον Μιλήσιο και τον Εύδοξο τον Κνίδιο. Ο διάλογος λέει πως ο Μάρκελλος κράτησε τον ένα από τους μηχανισμούς ως το μοναδικό προσωπικό λάφυρο από τις Συρακούσες και δώρισε τον άλλο στο Ναό της Αρετής στη Ρώμη. Ο μηχανισμός του Μάρκελλου παρουσιάστηκε από το Γάιο Σουλπίκιο Γάλλο στο Λούκιο Φούριο Φίλο πους τον περιέγραψε:
“Hanc sphaeram Gallus cum moveret, fiebat ut soli luna totidem conversionibus in aere illo quot diebus in ipso caelo succederet, ex quo et in caelo sphaera solis fieret eadem illa defectio, et incideret luna tum in eam metam quae esset umbra terrae, cum sol e regione“.
“Όταν ο Γάλλος μετακίνησε την υδρόγειο, τότε η Σελήνη ακολούθησε τον Ήλιο σ’ όσες στροφές κι αν έκανε σ’ αυτή τη μπρούντζινη συσκευή όπως θα γινότανε και στον ουρανό, από την οποία είδαμε ότι επίσης στον ουρανό η έκλειψη Ηλίου ήταν η ίδια όταν η Σελήνη ερχόταν σε κείνη τη θέση ώστε να ρίχνει τη σκιά της πάνω στη Γη, όταν τα 3 σώματα ήταν ευθυγραμμισμένα“.
Αυτή είναι η περιγραφή ενός πλανητάριου ή πλανητοσκοπίου. Ο Πάππος ο Αλεξανδρεύς δήλωσε ότι ο Αρχιμήδης είχε γράψει χειρόγραφο (σήμερα χαμένο) πάνω στη κατασκευή τέτοιων μηχανισμών με το τίτλο Περί σφαιροποιΐας. Πρόσφατες έρευνες σ’ αυτό το θέμα εστιάζουνε στον Μηχανισμό των Αντικυθήρων, άλλη μία συσκευή από τη κλασσική αρχαιότητα που πιθανότατα σχεδιάστηκε για τον ίδιο λόγο. Η δημιουργία τέτοιου είδους μηχανισμών θα απαιτούσε προχωρημένη γνώση για τη λειτουργία του διαφορικού. Αυτό πιστευόταν ότι ήτανε πέρα των δυνατοτήτων της τεχνολογίας στις αρχαίες εποχές, αλλά η ανακάλυψη του Μηχανισμού το 1902 επιβεβαίωσε το γεγονός ότι συσκευές τέτοιου είδους ήταν γνωστές στους αρχαίους Έλληνες.

Η ιστορία του χρυσού στέμματος δεν εμφανίζεται στα γνωστά έργα του Αρχιμήδη. Επιπλέον, η πρακτικότητα της μεθόδου που περιγράφει έχει αμφισβητηθεί, λόγω της υψηλής ακρίβειας που χρειάζεται κάποιος για να μετρήσει τη μετατόπιση νερού. Αντ’ αυτού αναζήτησε λύση της υδροστατικής που αναφέρεται ως η γνωστή αρχή του Αρχιμήδη, που ο ίδιος τη περιγράφει στο σύγγραμμα Περί επιπλέοντων σωμάτων. Αυτή η αρχή δηλώνει ότι ένα σώμα που βυθίζεται σε ρευστό δέχεται δύναμη άνωσης ίση με το βάρος του υγρού που εκτοπίζει. Χρησιμοποιώντας αυτή την αρχή, θα ‘τανε δυνατή η σύγκριση της πυκνότητας της χρυσής στεφάνης με κείνη του στερεού χρυσού με την εξισορρόπηση της κορώνας σε ένα ζυγό με δείγμα αναφοράς χρυσού και στη συνέχεια βυθίζοντας τη συσκευή στο νερό. Η διαφορά πυκνότητας μεταξύ των 2 δειγμάτων θα μπορούσε να προκαλέσει τη κλίμακα ν’ ανατραπεί αναλόγως.Ο Γαλιλαίος έκρινε ότι “πιθανολογείται ότι η μέθοδος αυτή είναι η ίδια που ακολούθησε ο Αρχιμήδης, δεδομένου ότι, εκτός του ότι είναι πολύ ακριβής, βασίζεται σ’ επιδείξεις που παρουσίασε ο Αρχιμήδης ο ίδιος“. Σε κείμενο του 12ου αι. με τίτλο Mappae clavicula υπάρχουν οδηγίες για το πώς να εκτελέσει κανείς τις ζυγίσεις στο νερό προκειμένου να υπολογίσει το ποσοστό του αργύρου που χρησιμοποιήθηκε κι ως εκ τούτου την επίλυση του προβλήματος. Το λατινικό ποίημα Carmen de ponderibus et mensuris του 4ου ή 5ου αι. περιγράφει τη χρήση της υδραυλικής ισορροπίας για τη λύση του προβλήματος της κορώνας κι αποδίδει τη μέθοδο στον Αρχιμήδη.
Παρ’ ότι δεν ήταν ο Αρχιμήδης που εφηύρε τον μοχλό, έδωσε μια εξήγηση για την αρχή που βασίζεται η χρήση του στο έργο του Περί επιπέδων Ισορροπιών. Αρχαιότερες περιγραφές του μοχλού μπορούν να βρεθούνε στη Περιπατητική Σχολή των υποστηρικτών του Αριστοτέλη και μερικές φορές αυτές αποδίδονται στον Αρχύτα. Σύμφωνα με τον Πάππο τον Αλεξανδρέα, το έργο του Αρχιμήδη πάνω στους μοχλούς τον έκανε να παρατηρήσει: “Δώστε μου ένα σημείο να στηριχθώ και θα κινήσω τη Γη” (δῶς μοι πᾶ στῶ καὶ τὰν γᾶν κινάσω). Ο Πλούταρχος περιγράφει πώς ο Αρχιμήδης σχεδίαζε ανυψωτικά συστήματα τροχαλιών επιτρέποντας στους ναυτικούς να χρησιμοποιούν την αρχή της μόχλευσης για να σηκώνουν αντικείμενα που ειδάλλως δεν θα μπορούσαν να σηκώσουνε. Στον Αρχιμήδη επίσης αποδίδεται η βελτίωση της δύναμης και της ακρίβειας του καταπέλτη καθώς κι η εφεύρεση του οδομετρητή στη διάρκεια του Α’ Καρχηδονιακού πολέμου. Ο οδομετρητής περιγράφεται σαν κάρρο με μηχανισμό γραναζιού που έριχνε μια μπάλα σ’ ένα κιβώτιο κάθε φορά που συμπλήρωνε ένα μίλι. Επίσης κατασκεύασε ένα υδραυλικό ρολόι που υπολόγιζε με μεγάλη ακρίβεια τις ώρες κι ειδοποιούσε για την αλλαγή της ώρας.
Ενώ συχνά θεωρείται ως σχεδιαστής μηχανικών συσκευών, ο Αρχιμήδης έκανε επίσης συνεισφορές στον τομέα των μαθηματικών. Ο Πλούταρχος έγραψε: “Αφιέρωσε όλη του τη στοργή και τη φιλοδοξία του σ’ αυτές τις καθαρότερες εικασίες όπου δεν μπορεί να γίνει αναφορά στις χυδαίες ανάγκες της ζωής“. Ο Αρχιμήδης χρησιμοποίησε το πυθαγόρειο θεώρημα για να υπολογίσει τη πλευρά του 12γωνου απ’ αυτή του 6γώνου και για κάθε επακόλουθο 2πλασιασμό των πλευρών του κανονικού πολυγώνου.
Ο Αρχιμήδης μπορούσε να χρησιμοποιήσει τα απειροελάχιστα με τρόπο παρόμοιο με τον ολοκληρωτικό λογισμό. Μέσω της εις άτοπον απαγωγής μπορούσε να δώσει απαντήσεις σε προβλήματα ως έναν αυθαίρετο βαθμό ακρίβειας, προσδιορίζοντας τα όρια που μέσατους ίσχυε η απάντηση. Αυτή η μέθοδος είναι γνωστή ως η μέθοδος της εξάντλησης και την εφάρμοσε για να προσεγγίσει τη τιμή του αριθμού π. Στο Κύκλου Μέτρησις το ‘κανε αυτό ζωγραφίζοντας ένα μεγαλύτερο κανονικό εξάγωνο έξω από τον κύκλο και ένα μικρότερο κανονικό εξάγωνο μέσα στο κύκλο και προοδευτικά διπλασιάζοντας τον αριθμό των πλευρών και στα δύο κανονικά πολύγωνα, υπολογίζοντας το μήκος της πλευράς κάθε πολυγώνου σε κάθε βήμα. Καθώς ο αριθμός των πλευρών αυξάνεται, γίνεται μια πιο ακριβής προσέγγιση του κύκλου. Μετά από 4 τέτοια βήματα, όταν τα πολύγωνα είχαν από 96 πλευρές το καθένα, ήταν σε θέση να προσδιορίσει ότι η τιμή του π βρισκόταν ανάμεσα στο 31⁄7 (περίπου 3,1429) και 310⁄71 (περίπου 3,1408) εντός των ορίων αφού η τιμή προσεγγιστικά είναι 3,1416. Επίσης απέδειξε ότι το εμβαδόν ενός κύκλου ισούται με το π πολλαπλασιασμένο με το τετράγωνο της ακτίνας του κύκλου (πr2). Στο Περί σφαίρας και κυλίνδρου δηλώνει ότι ένα μέγεθος όταν προστεθεί αρκετές φορές στον εαυτό του θα ξεπεράσει οποιοδήποτε άλλο μέγεθος. Αυτή είναι η Αρχιμήδεια ιδιότητα των πραγματικών αριθμών.

Στο Κύκλου μέτρησις. Σώζονται 3 θεωρήματα. Αυτή είναι σύντομη εργασία που αποτελείται από 3ς προτάσεις. Είναι γραμμένη σε μορφή αλληλογραφίας με τον Δοσίθεο του Πηλουσίου, που ήταν μαθητής του Κόνωνα του Σάμιου. επίσης, υποστηρίζει πως η τετραγωνική ρίζα του 3 βρίσκεται ανάμεσα στο 265⁄153 (περίπου 1,7320261) και στο 1351⁄780 (περίπου 1,7320512). Η πραγματική τιμή είναι περίπου 1,7320508, γεγονός που κάνει αυτό τον υπολογισμό πολύ ακριβή. Παρουσίασε αυτό το αποτέλεσμα χωρίς να προσφέρει καμμία εξήγηση για το πως έφτασε σε αυτό. Αυτή η όψη του έργου του ανάγκασε τον John Wallis να δηλώσει: «πιθανόν να κάλυψε τα ίχνη της ερευνάς του σκόπιμα επειδή θα ένιωθε ότι δίνει στους μεταγενέστερους το μυστικό της συλλογής πληροφοριών του, ενώ ταυτόχρονα ήθελε να αποσπάσει από αυτούς απαντήσεις για τα δικά του ευρήματα. “Είναι πιθανό να χρησιμοποιούσε επαναληπτικές διαδικασίες για να υπολογίσει αυτές τις τιμές“.
Στο Τετραγωνισμό της παραβολής. Στο έργο αυτό που αποτελείται από 24 προτάσεις ο Αρχιμήδης απέδειξε ότι το εμβαδόν που περικλείεται από μία παραβολή και μια ευθεία γραμμή είναι 4⁄3 φορές το εμβαδόν του αντίστοιχου εγγεγραμμένου τριγώνου. Εξέφρασε τη λύση στο πρόβλημα ως άπειρη Γεωμετρική σειρά με λόγο 1⁄4. Αν ο 1ος όρος σ’ αυτή τη σειρά είναι το εμβαδόν του τριγώνου, τότε ο 2ος είναι το άθροισμα των εμβαδών των 2 τριγώνων που οι βάσεις είναι οι δύο μικρότερες διατέμνουσες γραμμές κι ούτω καθεξής. Αυτή η απόδειξη χρησιμοποιεί μια παραλλαγή της σειράς 1/4 + 1/16 + 1/64 + 1/256 +… που ‘χει άθροισμα το 1⁄3. απευθυνόμενος στο Δοσίθεο, αποδεικνύει με 2 μεθόδους ότι το εμβαδόν που περικλείεται από μια παραβολή και μια ευθεία γραμμή ισούται με 4⁄3 πολλαπλασιαζόμενο επί το εμβαδό ενός τριγώνου με την ίδια βάση και ύψος. Αυτό το κατάφερε με τον υπολογισμό της αξίας της γεωμετρικής σειράς που αθροίζεται στο άπειρο με λόγο 1⁄4.
Στο Ψαμμίτη: Σ’ αυτή τη πραγματεία του,ξεκινά να υπολογίζει τον αριθμό των κόκκων άμμου που μπορούν να χωρέσουν μέσα στο σύμπαν. Στο βιβλίο αναφέρει την ηλιοκεντρική θεωρία του ηλιακού συστήματος που προτείνεται από τον Αρίσταρχο το Σάμιο, καθώς και σύγχρονες ιδέες σχετικά με το μέγεθος της Γης και την απόσταση μεταξύ διάφορων ουράνιων σωμάτων. Στη προσπάθεια του, αντιτάχθηκε στην ιδέα ότι ο αριθμός των κόκκων άμμου ήταν πολύ μεγάλος για να υπολογισθεί. Έγραψε: “Υπάρχουν μερικοί, βασιλιά Γέλωνα (Γέλων Β’, γιος του Ιέρωνα Β’) που πιστεύουν ότι ο αριθμός της άμμου είναι άπειρος σε μέγεθος και όταν λέω άμμου δεν εννοώ την άμμο που υπάρχει στις Συρακούσες και στην υπόλοιπη Σικελία αλλά και αυτή που βρίσκεται σε κάθε περιοχή είτε κατοικείται είτε όχι“. Για να λύσει το πρόβλημα, επινόησε ένα σύστημα μέτρησης με μονάδα μέτρησης τη μυριάδα. Η λέξη προέρχεται από τη λέξη μυριάς, για τον αριθμό 10.000. Πρότεινε ένα σύστημα αρίθμησης χρησιμοποιώντας μυριάδα μυριάδων (100 εκατομμύρια) και συμπέρανε πως ο αριθμός των κόκκων άμμου που χωρά το σύμπαν είναι 8 εικοσάκις εκατομμύρια ή 8 × 10^63. Ο Ψαμμίτης είναι το μόνο σωζόμενο έργο που συζητά τις απόψεις του σχετικά με την αστρονομία.
Οστομάχιον, είναι τεμαχισμένο παζλ παρόμοιο με tangram κι η πραγματεία που το περιέγραφε βρέθηκε σε πιο ολοκληρωμένη μορφή στο Παλίμψηστο του Αρχιμήδη. Υπολογίζει τα εμβαδά των 14ων κομματιών, που συναρμολογούμενα μπορούν να σχηματίσουνε 4γωνο. Έρευνα που δημοσιεύθηκε το 2003 από τον Δρ.Reviel Netz του Πανεπιστημίου Στάνφορντ, υποστήριζε πως ο Αρχιμήδης προσπαθούσε να καθορίσει με πόσους δυνατούς τρόπους θα μπορούσαν να τοποθετηθούν τα κομμάτια έτσι ώστε να συναρμολογήσουνε 4γωνο. Υπολογίζει πως τα κομμάτια μπορούν να δημιουργήσουνε τετράγωνο με 17.152 διαφορετικούς τρόπους. Ο αριθμός των διατάξεων είναι 536, όταν οι λύσεις που είναι ισοδύναμες με περιστροφή κι αντανάκλαση έχουν αποκλειστεί. Το παζλ αντιπροσωπεύει παράδειγμα πρώιμου προβλήματος στη Συνδυαστική. Η προέλευση του ονόματος του παζλ είναι ασαφής κι έχει υποστηριχθεί πως αυτό έχει ληφθεί από την αρχαία ελληνική λέξη για το λαιμό ή τον οισοφάγο, στόμαχος. Ο Αυσόνιος αναφέρεται στο παζλ, με την ονομασία Οστομάχιον, μια ελληνική σύνθετη λέξη που σχηματίζεται από τις ρίζες του ὀστέον (οστό) και της μάχης (αγώνας). Το παζλ είναι επίσης γνωστό ως Μικρό Πακέτο (loculus) του Αρχιμήδη ή Κουτί του Αρχιμήδη.
Περί σφαίρας και κυλίνδρου, Βιβλίο Α’ & Β’: Στη πραγματεία αυτή απευθυνόμενος στον Ευτόκιο Δοσίθεο, κατορθώνει κάτι που τον έκανε να ‘ναι ιδιαίτερα περήφανος. Αυτό ήταν η ανακάλυψη της σχέσης μεταξύ μίας σφαίρας κι ενός περιγεγραμμένου κυλίνδρου του ίδιου ύψους και της ίδιας διαμέτρου. Ο όγκος είναι 4⁄3πr^3 για τη σφαίρα, και 2πr^3 για τον κύλινδρο. Το εμβαδόν επιφανείας είναι 4πr^2 για τη σφαίρα, και 6πr^2 για τον κύλινδρο (συμπεριλαμβανομένων των 2 βάσεων), όπου r είναι η ακτίνα της σφαίρας και του κυλίνδρου. Η σφαίρα έχει όγκο τα 2/3 του περιγεγραμμένου κυλίνδρου. Ομοίως, η σφαίρα έχει εμβαδόν τα 2/3 του κυλίνδρου (συμπεριλαμβανομένων των βάσεων). Στον τάφο του Αρχιμήδη κατόπιν επιθυμίας του είχανε τοποθετηθεί 2 γλυπτά: μία σφαίρα κι ένας κύλινδρος.

Περί επιπέδων ισορροπιών ή κέντρα βαρών επιπέδων ή Μηχανικά, Βιβλίο Α’ & Β’: Το 1ο αποτελείται από 15 προτάσεις κι 7 αξιώματα, ενώ το 2ο περιέχει 10 προτάσεις. Σ’ αυτό το έργο του εξηγεί το Νόμο του Μοχλού δηλώνοντας ότι: “Τα μεγέθη είναι σε ισορροπία, όταν βρίσκονται σε αποστάσεις αντιστρόφως ανάλογες με το βάρος τους“. Ο Αρχιμήδης χρησιμοποιεί τις αρχές που προκύπτουνε, για τον υπολογισμό των εμβαδών και των κέντρων βάρους των διαφόρων γεωμετρικών σχημάτων, όπως τρίγωνα, παραλληλόγραμμα και παραβολές.
Περί ελίκων (28 προτάσεις, 6 πορίσματα) Αυτό το έργο των 28 προτάσεων, επίσης απευθυνόταν στον Δοσίθεο. Τούτη η πραγματεία ορίζει αυτό που σήμερα καλείται η σπείρα του Αρχιμήδη. Είναι ο γεωμετρικός τόπος των σημείων που αντιστοιχούνε στο σύνολο των διάφορων θέσεων, από τις οποίες διέρχεται ένα σημείο, με τη πάροδο του χρόνου, καθώς αυτό κινείται μακριά από ένα σταθερό σημείο με μια σταθερή ταχύτητα κατά μήκος μίας γραμμής, που περιστρέφεται με σταθερή γωνιακή ταχύτητα. Ισοδύναμα σε πολικές συντεταγμένες (r, θ) μπορεί να περιγραφεί απ’ την εξίσωση με πραγματικούς αριθμούς a και b. Αυτό είναι πρώιμο παράδειγμα μιας μηχανικής καμπύλης (καμπύλη που διαγράφεται από ένα κινούμενο σημείο), που θεωρείται από Έλληνα μαθηματικό.
Περί κωνοειδέων & σφαιροειδέων (32 προτάσεις, 1 πόρισμα) Αυτό είναι ένα έργο αποτελούμενο από 32 προτάσεις, που απευθύνονται στον Δοσίθεο. Σ’ αυτή τη πραγματεία του υπολογίζει τα εμβαδά και τους όγκους τμημάτων από κώνους, σφαίρες και παραβολοειδή. Ο υπολογισμός του εμβαδού επιφανειών ήτανε θέμα εργασιών από την αρχαιότητα. Τον 5ο αι. π.Χ. ο Εύδοξος είχε αναπτύξει τη μέθοδο της εξάντλησης σύμφωνα με τις ιδέες του Αντιφώντα. Στην μέθοδο αυτή, υποδιαιρούμε ένα σώμα σε πολύγωνα για να υπολογίσουμε το εμβαδόν του. Ο Εύδοξος ήδη είχε υπολογίσει το εμβαδόν ορισμένων πολύγωνων. Ο Αρχιμήδης βελτίωσε τη μέθοδο αυτή και κατάφερε να υπολογίσει το εμβαδόν της παραβολής.
Πρόβλημα Βοεικόν: το έργο ανακαλύφθηκε από τον Gotthold Ephraim Lessing σ’ ελληνικό χειρόγραφο αποτελούμενο από ένα ποίημα από 44 γραμμές, στη βιβλιοθήκη Herzog August στο Wolfenbüttel της Γερμανίας, το 1773. Απευθύνεται στον Ερατοσθένη και στους μαθηματικούς στην Αλεξάνδρεια. Ττους προκαλεί να μετρήσουνε τον αριθμό των βοοειδών στην Αγέλη του Ήλιου, με την ταυτόχρονη επίλυση ενός αριθμού Διοφαντικών εξισώσεων. Υπάρχει και μια πιο δύσκολη έκδοση του προβλήματος που μερικές από τις λύσεις απαιτείται να είναι τέλεια τετράγωνα. Αυτή η έκδοση του προβλήματος λύθηκε 1η φορά από τον Α. Amthor το 1880 κι η απάντηση είναι πολύ μεγάλος αριθμός, περίπου 7,760271 × 10206544.

Το κύριο έγγραφο που περιέχει το έργο του είναι το Παλίμψηστο του Αρχιμήδη. Το 1906, ο Δανός καθηγητής Johan Ludvig Heiberg επισκέφθηκε τη Πόλη κι εξέτασε περγαμηνή (από δέρμα κατσίκας), γραμμένη τον 13ο μ.Χ. αι., που περιείχε 174 σελίδες λειτουργικών κειμένων. Τελικά ανακάλυψε πως η περγαμηνή ήτανε παλίμψηστο, δηλαδή ένα έγγραφο με κείμενο που είχε γραφεί πάνω σε σβησμένη παλιά εργασία. Τα παλίμψηστα δημιουργούνταν ξαίνοντας το μελάνι από τα αρχικά έργα των περγαμηνών και την επαναχρησιμοποίηση τους. Αυτή ήτανε συνηθισμένη πρακτική στον Μεσαίωνα, καθώς η περγαμηνή ήταν αρκετά ακριβή. Τα παλιότερα έργα στο παλίμψηστο αναγνωρίστηκαν από τους μελετητές τον 10ο αι. μ.Χ., ως αντίγραφα από προηγούμενες άγνωστες πραγματείες του Αρχιμήδη. Η περγαμηνή, πριν να πωληθεί σε ιδιώτη συλλέκτη το 1920, ήτανε για εκατοντάδες χρόνια σε μια μοναστηριακή βιβλιοθήκη στη Πόλη. Στις 29 Οκτώβρη 1998, πωλήθηκε σε δημοπρασία σ’ ανώνυμο αγοραστή για 2.000.000 $ από τον Οίκο Κρίστις, στη Νέα Υόρκη.
Το παλίμψηστο λοιπόν αυτό είναι περγαμηνός κώδικας του 10ου αι., που περιέχει μαθηματικές πραγματείες. Το 1229 ο κώδικας υπέστη επεξεργασία, η γραφή σβήστηκε, τα φύλλα του αναδιατάχθηκαν, διπλώθηκανε στη μέση έτσι ώστε ένα παλιό φύλλο να αποτελέσει δύο ενός καινούργιου κώδικα και πάνω τους γραφτήκανε λειτουργικά κείμενα. Η απόξεση δεν ήταν ολοκληρωτική, με αποτέλεσμα υπό ευνοϊκές συνθήκες να διαφαίνεται το προηγούμενο κείμενο.
Το παλίμψηστο περιέχει 7 πραγματείες, συμπεριλαμβανομένου και του μοναδικού σωζόμενου αντιγράφου του έργου Περί επιπλεόντων σωμάτων στην αρχαία ελληνική. Είναι η μοναδική γνωστή πηγή του έργου Περί μηχανικών θεωρημάτων προς Ερατοσθένη έφοδος, που αναφερότανε στη Σούδα κι εθεωρείτο πως είχε χαθεί για πάντα. Το Οστομάχιον επίσης ήτανε στο παλίμψηστο, με μια πιο πλήρη ανάλυση του παζλ, σε σχέση με ό,τι είχε βρεθεί σε προηγούμενα κείμενα. Το παλίμψηστο είναι τώρα αποθηκευμένο στο Walters Art Museum της Βαλτιμόρης, Μέριλαντ, όπου υποβάλλεται σε διάφορων ειδών σύγχρονες δοκιμές, όπως η χρήση υπεριώδους ακτινοβολίας κι ακτίνων Χ, έτσι ώστε να διαβαστεί το αρχικό κείμενο. Ο Παλίμψηστος Κώδικας με την ονομασία Codex C, όπως τον αναφέρει ο Χάιμπεργκ, είναι η μόνη διασωζόμενη γνωστή πηγή που περιέχει αποσπάσματα από τις πραγματείες του. Σύμφωνα με τους γραφικούς χαρακτήρες του κειμένου χρονολογείται στον 10ο αι. μ.Χ. και πιστεύεται ότι πρόκειται γι’ αντιγραφή από κάποια αρχαιότερη πηγή, που δυστυχώς μάς είναι άγνωστη. Οι 7 πραγματείες του στο Παλίμψηστο είναι: Περί επιπέδων ισορροπιών, Περί ελίκων, Κύκλου μέτρησις, Περί σφαίρας και κυλίνδρου, Περί των επιπλεόντων σωμάτων, Περί μηχανικών θεωρημάτων προς Ερατοσθένη έφοδος και Οστομάχιον.
Πρόσφατα (2006) διαβάστηκαν από το Παλίμψηστο του Αρχιμήδη αποσπάσματα από τα έργα που διασώθηκαν σε αυτό:
Περί μηχανικών θεωρημάτων προς Ερατοσθένη έφοδος (=μέθοδος): Η πραγματεία αυτή θεωρείτο χαμένη μέχρι και την ανακάλυψη του Παλίμψηστου. Σ’ αυτή, χρησιμοποιεί απειροστικά και δείχνει πώς η διαμέλιση ενός σχήματος σ’ έναν άπειρο αριθμό, απείρως μικρών κομματιών, μπορεί να μας βοηθήσει στο να προσδιορίσουμε το εμβαδόν ή και τον όγκο του. Είχε υπόψη του πως αυτή η μέθοδος στερείται επίσημης αυστηρότητας, έτσι χρησιμοποίησε και τη μέθοδο της εξάντλησης για την εξαγωγή των αποτελεσμάτων. Όπως και το Πρόβλημα Βοοειδών, έτσι κι αυτό το έργο ήτανε γραμμένο με τη μορφή επιστολής προς τον Ερατοσθένη τον Αλεξανδρέα, Περί των επιπλεόντων σωμάτων: Στο 1ο μέρος αυτής της πραγματείας, εξηγεί το νόμο της ισορροπίας των υγρών κι αποδεικνύει πως το νερό θα υιοθετήσει μια σφαιρική μορφή γύρω από ένα κέντρο βαρύτητας. Αυτό μπορεί να ήταν μια προσπάθεια για να εξηγήσει τη θεωρία των τότε σύγχρονων Ελλήνων αστρονόμων, όπως και του Ερατοσθένη, ότι η Γη είναι σφαιρική. Τα υγρά περιγράφονται ως μη αυτοβαρυτικά, δεδομένου ότι υποθέτει την ύπαρξη ενός σημείου, προς το οποίο εμπίπτουν όλα τ’ αντικείμενα, με αποτέλεσμα ν’ αποκτούνε το σφαιρικό τους σχήμα.
Στο 2ο μέρος, υπολογίζει τις θέσεις ισορροπίας διάφορων τμημάτων από παραβολοειδή. Αυτό ήταν ίσως μια εξιδανίκευση των σχημάτων, που δημιουργούσε το βυθισμένο μέρος των πλοίων στο νερό. Κάποια από αυτά τα τμήματα επιπλέουν με τη βάση κάτω από το νερό και τη μέγιστη (σε ύψος) κορυφή πάνω από το νερό, παρόμοια με τον τρόπο με τον οποίο τα παγόβουνα επιπλέουν. Η αρχή της άνωσης του Αρχιμήδη παρατίθεται σε αυτό το έργο, ως εξής: “Κάθε σώμα που είναι εξ ολοκλήρου ή μερικώς βυθισμένο σε ρευστό, δέχεται μια ώθηση ίση σε μέγεθος, αλλά αντίθετης φοράς, με το βάρος του εκτοπισμένου ρευστού”.
Απόκρυφα έργα/Βιβλίο λημμάτων: Το έργο αυτό (ή Liber Assumptorum) είναι μια πραγματεία με 15 προτάσεις σχετικά με τη φύση των κύκλων. Το αρχαιότερο γνωστό αντίγραφο του κειμένου είναι στα αραβικά. Οι μελετητές T. L. Heath και Marshall Clagett υποστήριζαν πως δεν μπορεί να έχει γραφτεί από τον Αρχιμήδη, αυτό το έργο στη σημερινή του μορφή, δεδομένου ότι τον αναφέρει σε 3ο πρόσωπο, γεγονός που υποδηλώνει επεξεργασία από κάποιο άλλο συντάκτη. Το έργο αυτό μπορεί να βασίζεται σε μια προηγούμενη εργασία του που πιθανότατα έχει χαθεί. Επίσης, θεωρείται πως ο Τύπος του Ήρωνα για τον υπολογισμό του εμβαδού ενός τριγώνου από το μήκος των πλευρών του, ήτανε γνωστός στον Αρχιμήδη. Ωστόσο, η 1η αξιόπιστη αναφορά στον τύπο δίνεται από τον Ήρωνα τον Αλεξανδρέα τον 1ο μ.Χ. αι..

Η ανακάλυψη του χειρογράφου έχει περιπετειώδη ιστορία. Το 10ο αι., στη Πόλη, ένας ανώνυμος γραφέας αντέγραψε πραγματεία του Αρχιμήδη πάνω σε περγαμηνή, κρατώντας τα ελληνικά του πρωτοτύπου. Το 13ο αι., ένας μοναχός έσβησε το κείμενο, έκοψε τις σελίδες, περιέστρεψε τα φύλλα 90 μοίρες και τα δίπλωσε στη μέση. Η περγαμηνή στη συνέχεια ανακυκλώθηκε μαζί με περγαμηνές από άλλα βιβλία, για να δημιουργηθεί ένα προσευχητάριο. Πρώτος ανέφερε την ύπαρξή του ο ιστοριοδίφης Αθανάσιος Παπαδόπουλος-Κεραμεύς το 1899. Το παλίμψηστο ανήκε στη Βιβλιοθήκη του Μετοχίου του Παναγίου Τάφου στη Πόλη κι είχε μεταφερθεί εκεί από τη Σκήτη του Αγίου Σάββα στη Παλαιστίνη. Ο μεγάλος αναζητητής χειρογράφων Κονσταντίν φον Τίσεντορφ, που ανακάλυψε τον Σιναϊτικό Κώδικα, την επισκέφθηκε το 1846 κι είδε το χειρόγραφο αλλά δεν αναγνώρισε το περιεχόμενό του. Απέσπασε μόνο ένα 2φυλλο, που κατέληξε στη Βιβλιοθήκη του Καίμπριτζ (Ms. Add. 1879.23). Ούτε κι ο Παπαδόπουλος-Κεραμεύς μπόρεσε να διαβάσει τον κώδικα, κατάλαβε όμως ότι πρόκειται για κάποιο σημαντικό μαθηματικό έργο. Η είδηση έφτασε στον Δανό φιλόλογο Γιόχαν Χάιμπεργκ (Johan Ludwig Heiberg), που εξέδιδε τα έργα του Αρχιμήδη. Ο Χάιμπεργκ, παρά τη προχωρημένη του ηλικία, ταξίδεψε στη Πόλη το 1906 για να δει τον κώδικα. Από τη μελέτη του προέκυψε ότι ο κώδικας περιείχε αριθμό έργων του Αρχιμήδη γνωστών από άλλα χειρόγραφα και μαζί μ’ αυτά την επιστολή με τον τίτλο Περί των μηχανικών θεωρημάτων προς Ερατοσθένη έφοδος (ή απλά Μέθοδος), που δε διασώζεται σε κανέν άλλο χειρόγραφο και που την ύπαρξη ο επιστημονικός κόσμος γνώριζε μόνο από μια απλή αναφορά.
Στις ταραγμένες συνθήκες στη διάρκεια και μετά τον Α’ Παγκ. Πόλ., το παλίμψηστο ξέφυγε από τη κατοχή της Βιβλιοθήκης του Μετοχίου και εξαφανίστηκε, μέχρι που το 1998 βρέθηκε να πωλείται σε πλειστηριασμό του οίκου Christie’s στη Νέα Υόρκη. Όταν έγινε γνωστή η είδηση στην Ελλάδα, υπήρξε κινητοποίηση από το Υπουργείο Πολιτισμού κι από πνευματικά ιδρύματα της χώρας για να συγκεντρωθεί το απαιτούμενο ποσόν. Στις 28 Οκτωβρίου του 1998, η Ελλάδα έχασε την ευκαιρία να αποκτήσει το Παλίμψηστο. Παράλληλα το Πατριαρχείο Ιεροσολύμων κινήθηκε δικαστικά, ζητώντας να του αποδοθεί ο κώδικας, με την αιτιολογία ότι είχε κλαπεί από τη βιβλιοθήκη του Μετοχίου του στη 10ετία του ’20. Η δικαστική απόφαση δικαίωσε τον ιδιώτη ιδιοκτήτη Ρομπέρ Γκυερσάν (Robert Guersan), κληρονόμο ενός κάποιου Μαρί Λουί Σιριέ (Marie Louis Sirieix), που ‘χε ταξιδέψει στην Ελλάδα και τη Τουρκία στη 10ετία του ’20 κι είχε πεθάνει το 1956. Τελικά ο κώδικας άλλαξε χέρια για 2.000.000 $ και περιήλθε σε κάποιον ανώνυμο συλλέκτη, που το παρέδωσε στο Μουσείο Τέχνης Ουώλτερς (Walters Art Museum) της Βαλτιμόρης για συντήρηση, ψηφιοποίηση και μελέτη. Τον Αύγουστο του 2006, ομάδα επιστημόνων υπό την εποπτεία του φυσικού Ούβε Μπέργκμαν κατόρθωσε να φέρει στο φως ολόκληρο το κείμενο του εγγράφου. Αυτό που έχασε, δυστυχώς, η ελληνική Πολιτεία, το κέρδισε ευτυχώς η ανθρωπότητα. Το σημαντικότερο επιστημονικό χειρόγραφο που πουλήθηκε ποτέ σε δημοπρασία αποκαλύπτει 13 χρόνια αργότερα, χάρη στη σύγχρονη τεχνολογία και την αφοσίωση των ερευνητών ενός αμερικανικού μουσείου, τα μυστικά της μεγαλύτερης μαθηματικής ιδιοφυΐας του αρχαίου κόσμου.
Lost & Found: The Secrets of Archimedes είναι ο τίτλος της έκθεσης που εγκαινιάζεται στις 16 Οκτώβρη στο Μουσείο Τέχνης Walters της Βαλτιμόρης. Με φωτογραφίες, κείμενα και πολυμέσα, η έκθεση αφηγείται τη συναρπαστική περιπέτεια του σπάνιου χειρογράφου και το τεράστιο πρότζεκτ της συντήρησης, ψηφιακής επεξεργασίας και μελέτης του, που αποδεικνύει πως ο Αρχιμήδης ανακάλυψε τα μαθηματικά του απείρου, τη μαθηματική φυσική και τη συνδυαστική -κλάδος των μαθηματικών που χρησιμοποιείται στη πληροφορική.

Το 1999, ο ανώνυμος συλλέκτης που απέκτησε το Παλίμψηστο το παραχώρησε στο Μουσείο Walters και μια ομάδα ερευνητών ξεκίνησε τη προσπάθεια να διαβάσει τα σβησμένα κείμενα στο παλαιότερο σωζόμενο αντίγραφο του αρχαίου Ελληνα μαθηματικού, φυσικού, εφευρέτη, μηχανικού κι αστρονόμου. Οταν το Μουσείο Walters παρέλαβε το χειρόγραφο, πολλοί πίστευαν ότι δεν μπορούσε να ανακτηθεί τίποτε απ’ αυτό. “Ητανε σε φρικτή κατάσταση, έχοντας βάρος χιλίων ετών, των μετακινήσεων και της κακής χρήσης“, είπε ο διευθυντής του Πρότζεκτ Αρχιμήδης κι επιμελητής χειρογράφων και σπάνιων βιβλίων του Walters, Γουίλ Νόελ. 4 έτη χρειάστηκαν οι συντηρητές για να διαλύσουνε το βιβλίο, λόγω της εύθραυστης κατάστασης της περγαμηνής, που ‘χε καταστραφεί από μούχλα, ενώ κάποια σημεία είχανε σκεπαστεί με σύγχρονη συνθετική κόλλα! “Κατέγραψα τα πάντα κι έσωσα ακόμη και τα πιο μικροσκοπικά κομμάτια του χειρογράφου, φλούδες χρώματος, νήματα, σταθεροποίησα τη μελάνη με ζελατίνη, έκανα αμέτρητες επιδιορθώσεις με γιαπωνέζικο χαρτί“, εξηγεί η Αμπιγκέιλ Κουάντ, επικεφαλής του τμήματος συντήρησης χειρογράφων του αμερικανικού μουσείου.
Το 2000, μια ομάδα ερευνητών άρχισε την ανάκτηση των σβησμένων κειμένων. Χρησιμοποίησαν τεχνικές απεικόνισης σε διαφορετικά μήκη κύματος του υπέρυθρου, ορατού κι υπεριώδους φωτός (πολυφασματική απεικόνιση). Χάρη σε διαφορετικές μεθόδους ψηφιακής επεξεργασίας, το κείμενο αποκαλύφθηκε στα μάτια των ερευνητών με τρόπο που κανείς δεν το είχε δει 1000 έτη. Ενα μέρος του βιβλίου που είχε σκεπαστεί με ρύπους διαβάστηκε με ακτίνες Χ στο εργαστήρι Stanford Synchrotron Radiation Lightsource (SSRL). Ο Αρχιμήδης, στη πραγματεία του Περί μεθόδου των θεωρημάτων μηχανικής ασχολείται με την έννοια του απόλυτου απείρου και το Παλίμψηστο περιέχει το μόνο σωζόμενο αντίγραφο του σημαντικού συγγράμματος. Ο αρχαίος Έλληνας μαθηματικός ισχυρίζεται ότι 2 διαφορετικά σύνολα γραμμών είναι ίσα σε πλήθος, αν κι είναι σαφώς κατανοητό πως είναι άπειρα. Η προσέγγιση αυτή είναι όμοια με έργα του 16ου και του 17ου αι., που οδήγησαν στην επινόηση του λογισμού. Επίσης, μόνο στο Παλίμψηστο βρέθηκε το Οστομάχιον, η αρχαιότερη πραγματεία περί συνδυαστικής. Θεωρείται ότι προσπαθούσε να ανακαλύψει με πόσους τρόπους θα μπορούσε να ανασυνδυάζει 14 τμήματα και να κάνει ένα τέλειο τετράγωνο. Η απάντηση είναι: 17.152 συνδυασμούς. Η συνδυαστική θεωρείται ζωτικής σημασίας στη πληροφορική.
Εκτός από τα έργα του Αρχιμήδη, στο Παλίμψηστο βρέθηκαν επίσης κρυμμένα: ένα σχόλιο πάνω στις Κατηγορίες του Αριστοτέλη, καθώς και κείμενα του Υπερείδη, Αθηναίου ρήτορα του Χρυσού Αιώνα. Οταν το Παλίμψηστο οδηγήθηκε στο SSRL, αποκαλύφθηκε στη 1η σελίδα κι η ταυτότητα του γραφέα που ‘σβησε τα γραπτά του Αρχιμήδη. Τ’ όνομά του ήταν Ιωάννης Μύρωνας και τελείωσε τη μεταγραφή των προσευχών στις 14 Απρίλη 1229, στην Ιερουσαλήμ.

* Υπάρχει ένας κρατήρας στη Σελήνη με το όνομα του Αρχιμήδη (29.7° Β, 4.0° Δ)προς τιμή του, καθώς και μια σεληνιακή οροσειρά, Τα Βουνά του Αρχιμήδη (25.3° Β, 4.6° Δ).
* Ο αστεροειδής της κύριας ζώνης αστεροειδών, με προσωρινή ονομασία 1987 SL7, πήρε το όνομα 3600 Αρχιμήδης από αυτόν.
* Το μετάλλιο Fields για εξαιρετικές επιδόσεις στα μαθηματικά φέρει πορτραίτο του Αρχιμήδη, μαζί με σκάλισμα απεικονίζει την απόδειξη στη σφαίρα και τον κύλινδρο.Η επιγραφή γύρω από το κεφάλι του είναι απόσπασμα που αποδίδεται σ’ αυτόν και γράφει στα λατινικά: “Transire suum pectus mundoque potiri” (Ανέβα πάνω από τον εαυτό σου και κατάκτησε τον κόσμο).
* Ο Αρχιμήδης έχει αποτυπωθεί στα γραμματόσημα που εκδίδονται από την Ανατολική Γερμανία (1973), Ελλάδα (1983), Ιταλία (1983), τη Νικαράγουα (1971), Σαν Μαρίνο (1982), και την Ισπανία (1963).
* Το επιφώνημα του Εύρηκα! που αποδίδεται στον Αρχιμήδη είναι το σύνθημα της πολιτείας της Καλιφόρνια. Στη περίπτωση αυτή η λέξη αναφέρεται στην ανακάλυψη χρυσού κοντά στο Σάττερς Μιλ το 1848 που πυροδότησε τον πυρετό του χρυσού εκεί.
* Ένα κίνημα με πολιτική συμμετοχή,που αποσκοπεί στη καθολική πρόσβαση στην υγειονομική περίθαλψη στη πολιτεία Όρεγκον έχει ονομαστεί Κίνημα Ο Αρχιμήδης, μ’ επικεφαλής τον πρώην Κυβερνήτη του Όρεγκον John Kitzhaber.
ΔΙΑΣΩΘΕΝΤΑ ΕΡΓΑ ΤΟΥ:
· “Περί σφαίρας και κυλίνδρου” Βιβλίο α’ και β’
· “Κύκλου μέτρησις” Σώζονται τρία θεωρήματα.
· “Περί κωνοειδέων και σφαιροειδέων” (32 θεωρήματα, 1 πόρισμα)
· “Περί ελίκων” (28 θεωρήματα, 6 πορίσματα)
· “Περί επιπέδων ισορροπιών ή κέντρα βαρών επιπέδων ή Μηχανικά” Βιβλ α’ και β’.
· “Βιβλίο λημμάτων”
· “Πρόβλημα Βοεικόν”
· “Κατασκευή πλευράς του περιγραφομένου εις κύκλο επταγώνου”
· “Ωρολόγιον Αρχιμήδους” (Σώζεται στα αραβικά)
· “Περί κύκλων εφαπτομένων αλλήλων”
· “Αρχαί της Γεωμετρίας”
· “Ψαμμίτης”
· “Τετραγωνισμός παραβολής”
· Πρόσφατα (2006) διαβάστηκαν από το Παλίμψηστο του Αρχιμήδη αποσπάσματα από τα έργα που διασώθηκαν σ’ αυτό:
· “Οστομάχιον”
· “Περί μηχανικών θεωρημάτων προς Ερατοσθένη έφοδος (=μέθοδος)
· “Περί των επιπλεόντων σωμάτων”
· “Οχουμένων” (Υδροστατική επιπλεόντων σωμάτων)
Συγγράμματα μη διασωθέντα · (ή συγγράμματα μη αποκαλυφθέντα μέχρι σήμερα)
· “Αριθμητικά”
· “Βαρουλκός, Υδροσκοπίαι, Πνευματική”
· “Επισίδια Βιβλία” (Μάλλον περί στατιστικής -Τζέτζης)
· “Περί τριγώνων”
· “Περί τετραπλεύρου”
· “Περί ζευγών”
· “Περί 13 ημικανονικών πολυέδρων”
· “Ισοπεριμετικά”
· “Ισορροπίαι”
· “Καύσις δια κατόπτρων” (επ΄ αυτού έγινε επιτυχές πείραμα στο Ν.Σ.)
· “Περί Αρχιτεκτονικής”
· “Περί βαρύτητος και ελαφρότητος (Πυκνόμετρα – Αραιόμετρα)
· “Περί δρομομέτρων” (Οδόμετρα πλοίων)
· “Περί κέντρου Βάρους ή Κεντροβαρικά”
· “Κατοπρικά”
· “Περί παραλλήλων γραμμών”
· “Περί κοίλων και παραβολικών κατόπτρων”
· “Προοπτική”
· “Στοιχεία μηχανικών”
· “Πλινθίδες και Κύλινδροι”
· “Στοιχεία επί των στηρίξεων”
· “Σφαιροποιΐα”
Εφευρέσεις
· “Αστρονομική συσκευή”
· “Βαρουλκός”
· “Γερανοί” (Αρπάγες)
· “Καταπέλτες”
· “Κάτοπτρα”
· “Κοχλίας ή έλιξ”
· “Οδόμετρο (δρομόμετρο)”
· “Πλανητάριον (σφαίρα)
· “Πολύσπαστον” (Βαρούλκο), “τρίσπαστο”
· “Σίφων”
· “Οστομάχιον” (επιτραπέζιο παιγνίδι το πρώτο πάζλ)
· “Τηλεβόλον Αρχιμήδους”
· “Χαριστίων” (μοχλός)
· “Ωρολόγιο υδραυλικό”





